UPlift Model

根据 [[营销人群四象限]]，应该针对 TR 人群进行营销活动。

Uplift 干预和不干预的差值

• 响应模型 Response Model，预测干预情况下用户是否购买

  • $\text { Outcome }=P(\text { buy } \mid \text { treatment })$

• uplift 通过干预和不干预的反事实来预估计算因果效应

  • $\text { Lift }=P(\text { buy } \mid \text { treatment })-P(\text { buy } \mid \text { no treatment })$

  • $\tau=Y(1)-Y(0)$

• 样本服从CIA ( [[Conditional Independence Assumption]] ) 条件独立假设

$\tau=Y(1)-Y(0)$ 通过随机对照实验收集数据：实验组全部干预，对照组都不干预。

• 利用条件平均因果效应[[CATE]]来预估给定条件下用户群体的平均因果效应

  • $\begin{aligned} \tau & =E[Y(1)-Y(0) \mid X] \\ & =E[Y(1) \mid X]-E[Y(0) \mid X] \\ & =E[Y(1) \mid T=1, X]-E[Y(0) \mid T=0, X]\end{aligned}$

• 利用一个人群的条件平均因果效应去近似个体因果效应

核心问题

• 混杂因素偏置 Confounding Bias

  • 干预机制导致选择偏差

• 归纳偏置

  • CATE 干预打分-非干预打分差值

模型方案

• [[Meta-Learner]]

  • [[S-Learner]] one-model 的差分响应模型
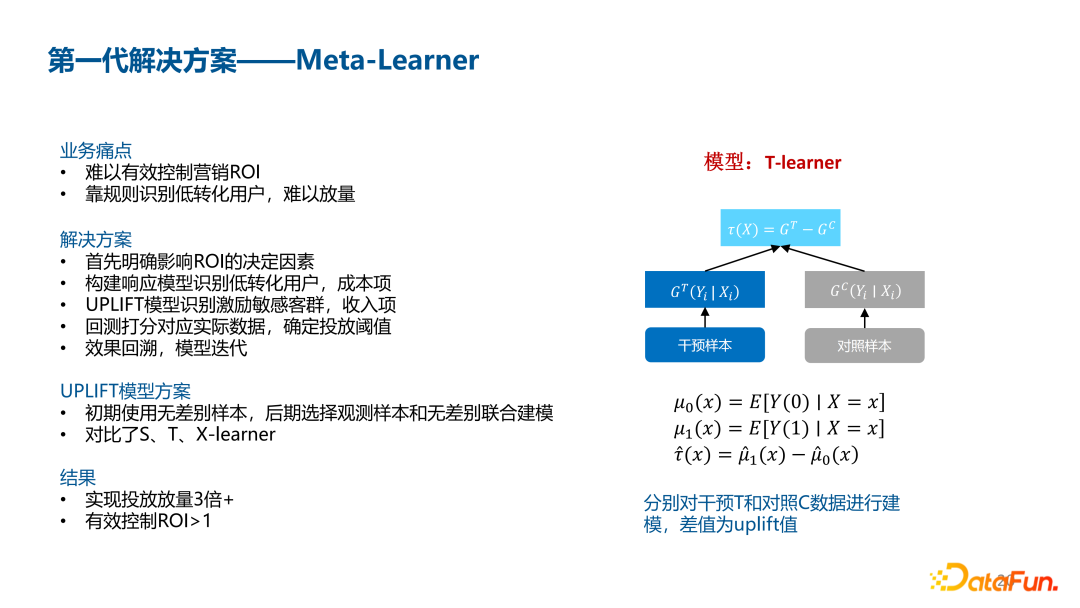
  • [[T-Learner]] two-model 差分响应模型
  • [[X-Learner]] 基于 T-Learner的反事实推断模型
    

• CRFnet 和 EFIN （[[Explicit Feature Interaction uplift Network]]）

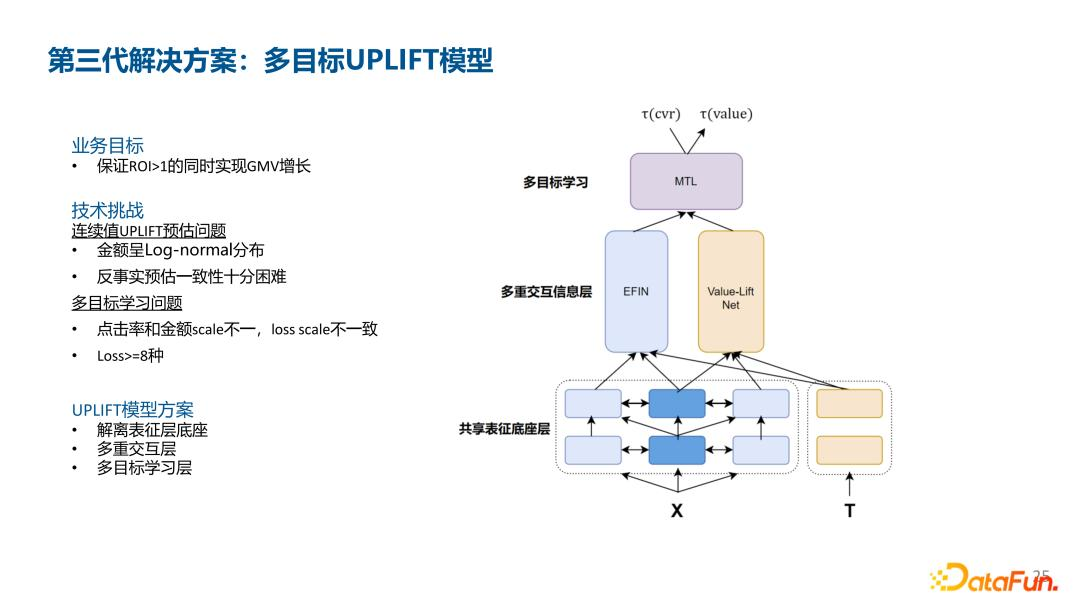
• 多目标 uplift 模型

[[Uplift Model 评估]] 不可能同时观察到同一个用户在不同干预策略下的响应，即使无法获取用户真实增量，无法用常规分类和回归问题的评估指标。

• 通过划分十分位数来对齐实验组和对照组数据去进行间接评估

• [[Qini curve]]

• [[AUUC]]